Next: Boundary-layer Thickness, Skin friction,
Up: Similarity Solution.
Previous: Vorticity.
The normal components of the stress perpendicular and parallel to the flat plate expressed non-dimensionally are
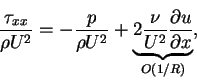 |
(68) |
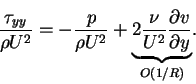 |
(69) |
Therefore, in the limit
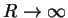 ,
we have that
,
we have that
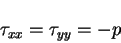 |
(70) |
The shearing stress over surfaces parallel to the wall is
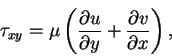 |
(71) |
which is approximated in the same way as the vorticity, as follows.
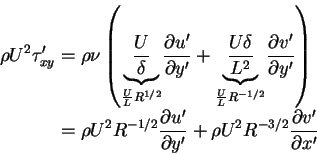 |
(72) |
In the limit
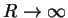 ,
the shear stress is given by
,
the shear stress is given by
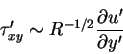 |
(73) |
or in terms of dimensional variables
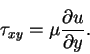 |
(74) |
For the Blasius laminar boundary layer similarity solution given by equation (3.47), the shear stress 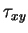 is given by
is given by
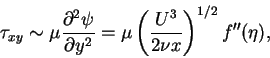 |
(75) |



Next: Boundary-layer Thickness, Skin friction,
Up: Similarity Solution.
Previous: Vorticity.
Karl P Burr
2003-03-12