![]() Disclaimer: A
knot is not mathematically well defined in an open chain,
Disclaimer: A
knot is not mathematically well defined in an open chain,
and its "size" is ambiguous, yet ...
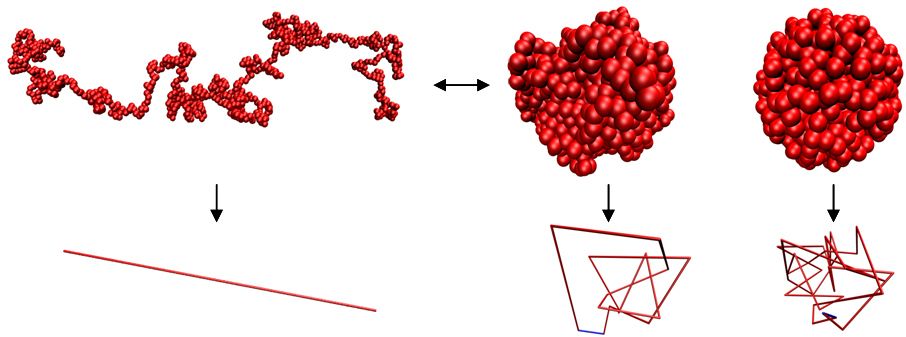
![]() Pulling
knots: Knots can be tied by pulling
on the ends of a chain.
Pulling
knots: Knots can be tied by pulling
on the ends of a chain.
- E.g., in experiments on single DNA
molecules:
- X.R. Bao, H.J. Lee, and S.R. Quake, PRL91, 265506 (2003)
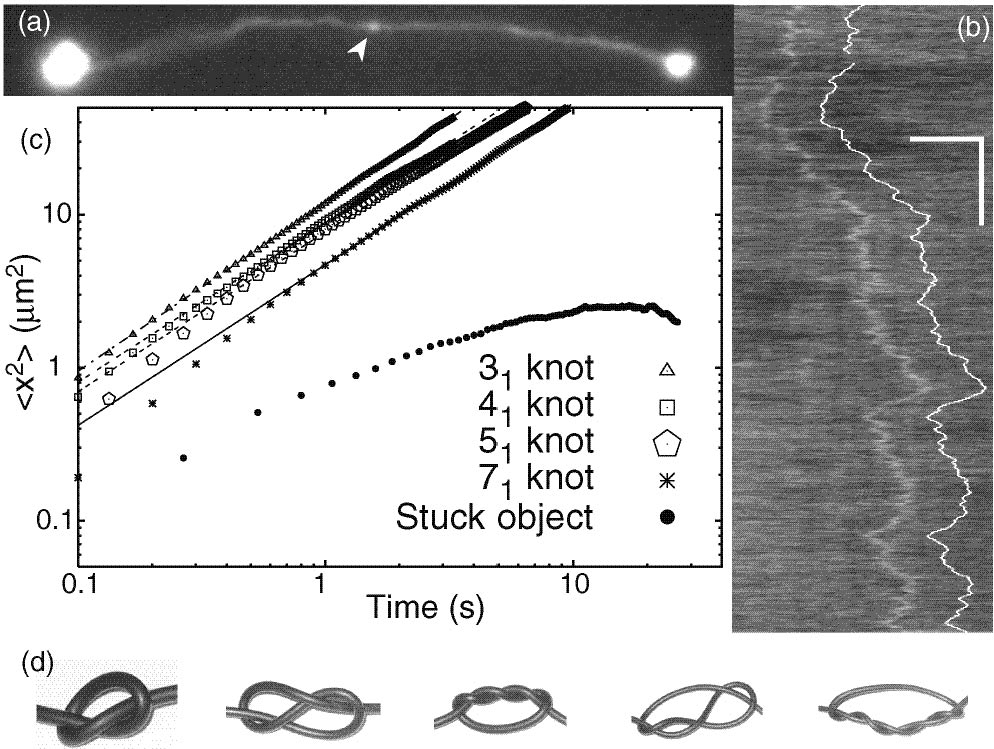
- In control experiments ... (knots) were present about 10% of the time, ...
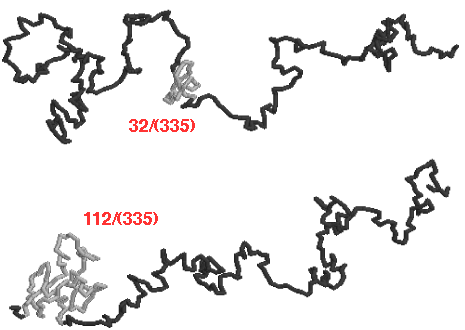
![]() We
used simulations of pulled knots to estimate the size:
We
used simulations of pulled knots to estimate the size:
- O. Farago, Y. Kantor and M. Kardar, Europhys. Lett. 60, 53 (2002)
- Scaling theory predicts that for an unknotted polymer of length N
![]()
- Comparison of simulation results for sizes N=225 (diamonds), 335 (triangles), 500 (squares), 750 (circles), with (solid) and without (open) a knot in the polymer:
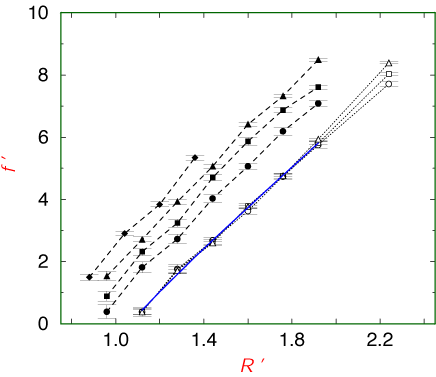
- Interestingly,
the correction to scaling exponent of 0.56 in d=3
is consistent with t=0.4
 0.1.
0.1.
- However,
a recent study
claims t=0.75
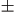 0.14.
0.14.
- B. Marcone, E. Orlandini, A.L. Stella, and F. Zonta (cond-mat/040523)
- However,
a recent study
claims t=0.75
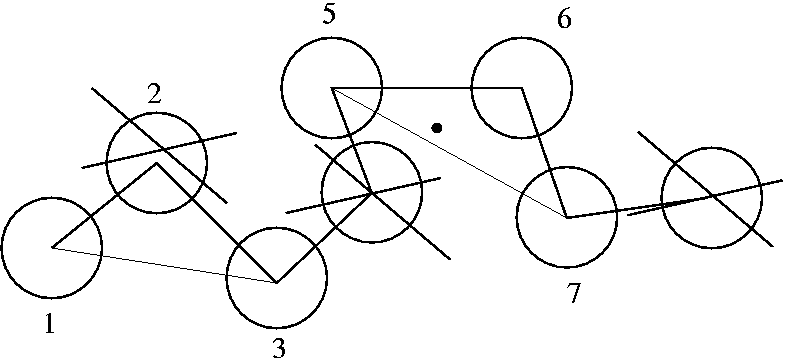
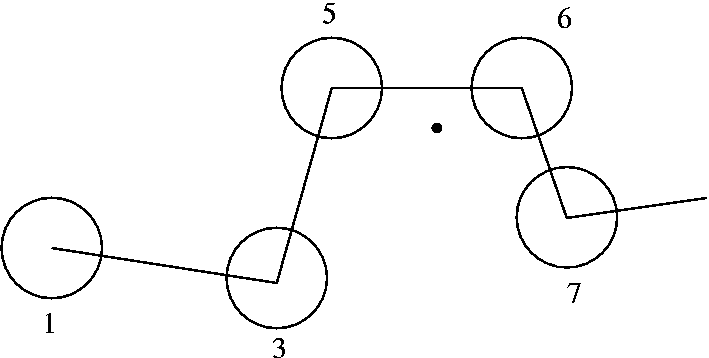
![]() Reducing
complexity: To find and localize knots in long open polymers
Reducing
complexity: To find and localize knots in long open polymers
- Close the chain by connecting its end through a number of procedures, and look for knots.
-
A simplification (reduction) step is essential for calculation of Alexander polynomials
- K. Koniaris and M. Muthukumar, Phys. Rev. Lett. 66, 2211 (1991)
- W.R. Taylor, Nature 406, 916-919 (2004)