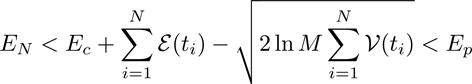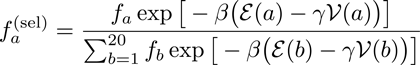Model & Analysis
Focus on the energetics of binding of TCR to peptide:
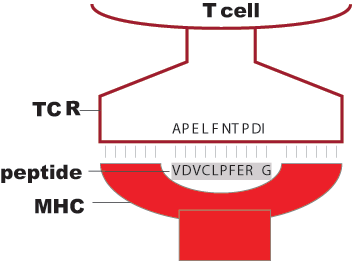
Assume a pairwise interaction between the peptide amino-acids and corresponding ones on the TCR, resulting in binding energy
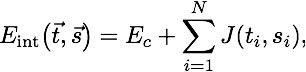(Miazawa-Jernigan matrix J)
A. Kosmrlj, A. Jha, E.S. Huseby, M. Kardar, & A.K. Chakraborty, PNAS 105, 16671 (2008) (offlline)
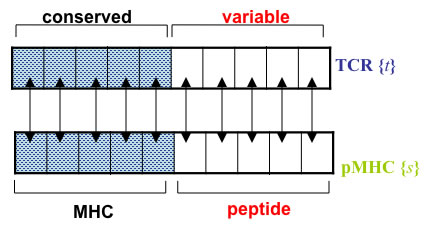
Thymic selection of TCRs is modeled using the interaction E as follows:
Candidate TCR sequences are randomly generated. (This ignores potential V(D)J generation bias.)
The binding energy of any TCR is calculated against a repertoire of M self-peptides.
(Experimental justification)
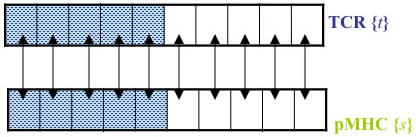
The selection condition is equivalent to the choice of the Extreme Value:
Characteristics of the Extreme Value Distribution .gif)
:
Binding energies of a particular TCR sequencs:
Extremal mean value: 
~ .gif)
,
where .gif)
and .gif)
are the mean and variance of interactions of the candidateTCR sequence.
Extremal standard deviation: 
~ .gif)
Note scaling in the large N limit; 
(proteome)
Due to the shaprpness of the distibution in the large N limit, the seletion condition can be written as:
[ and are the mean and variance of interactions of the candidate TCR sequence.]
The above selection condition is reminiscent of the micro-canonical constraints in Statistical Physics.
The "energy" involves interactions amongst the N amino-acids in the sequence 
The "interaction" depends only on the sum of variances for the individual amino-acids
As such, in the large N limit, the probability to select a sequence can be written as a product
,
where 
and 
have to be obtained self-consistently from
and 
.
Graphical solution for
0.gif)
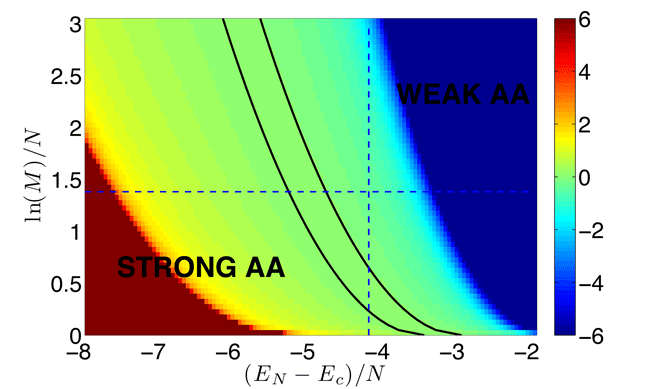
Because of the restriction to an energy interval, there is a range of parameters where = 0.
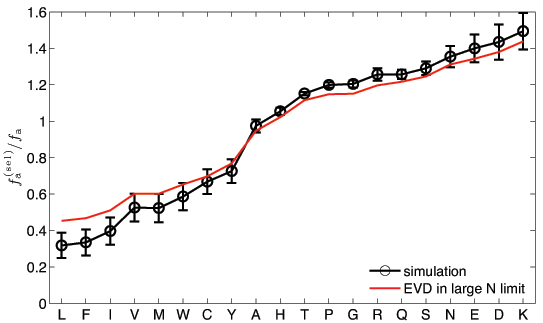
How well does this work for finite N? (N=5 and M=10.000)
A. Kosmrlj, A.K. Chakraborty, M.K., & E. Shakhnovich, PRL 103, 068103 (2009)
