Fluctuations of Force

red ball The force from fluctuations is itself a fluctuating quantity; best manifested for a small object, such as a Brownian particle

=====>

red ball QED analog: Small polarize particle in vacuum zero temperature, subject to quantum fluctuations of the electromagnetic field;

 Dynamic Casimir phenomena: Force fluctuations and friction act on accelerating bodies in vacuum even at zero temperature.

yellow ball "Quantum Theory of the Electromagnetic Field in a Variable-Length One-Dimensional Cavity,"

G. T. Moore, J. Math. Phys. 11, 2679 (1970)

yellow ball "Radiation from a Moving Mirror in Two Dimensional Space-Time: Conformal Anomaly,"

S. A. Fulling and P. C. W. Davies, Proc. R. Soc. London, Ser. A 348, 393 (1976).

yellow ballLangevin equation for an otherwise free particle,

yellow ball For a charged particle, the force is linearly coupled to the bath

However, a linear coupling is forbidden for a neutral, but polarize, particle.

yellow ball With linear coupling, a free field theory implies a Gaussian distribution for φ,

hence the force and the displacement are also Gaussian distributed, entirely described by the variance

yellow ball For a neutral particle (no linear coupling), the quadratic force is not Gaussian distributed; leading to cumulants

consistent with a power-law probability distribution, reminiscent of Levy flights:

yellow ball "Flight of a heavy particle nonlinearly coupled to a quantum bath,"

M.F. Maghrebi, M. Kruger, & M. Kardar, PRB 93, 014309 (2016). 

 

 

 

 

 

 

 

 

 

 

 

red ballRotational friction: Consider waves of frequency ω and angular state m impinging on object rotating with frequency Ω

Lab frame:           

Object frame:         

yellow ball "Generation of waves by a rotating body,"

Ya B. Zel'dovich, JETP Lett. 14, 180 (1971);  If  ω' and  ω have opposite signs:

 yellow ball  Amplitude of (classical) scattered wave exceeds incoming wave (Super-radiance).

 yellow ball  Conjectured (quantum) spontaneous emission with no incoming wave.

yellow ball "Spontaneous emission by rotating objects: A scattering approach,"

M.F. Maghrebi, R.L. Jaffe, & M. Kardar, PRL108, 230403 (2012). 

yellow ballNumber of photons in a mode of frequency ω and angular momentum m,

generated by object rotating with angular velocity Ω  is:

        

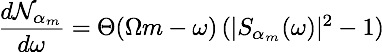
yellow ballE.g., net power for a rotating cylinder:  

BBT  (url)