Engine (work & efficiency)

 Near field: For simplicity, let us consider a material with a single dominant frequency   ,

where the propulsive force and heat transfer in the near-field regime can be estimated as

        , 

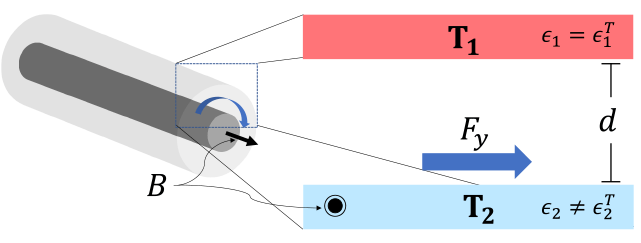
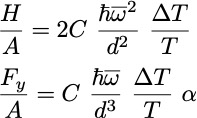where C  is dimensionless, and  is a measure of asymmetry, e.g..    in a magnetic field.

 Work can be extracted from the motive force, only if the plate is moves with some velocity  v

yellow ball Naively, from the extracted power, the engine efficiency is given by

yellow ball The above formula may suggest exceeding the Carnot efficiency for velocities greater than

The Rytov formalism combined with Linear response relations, provides the needed corrections:

yellow ball Heat emitted by a moving body is larger than when at rest:

yellow ball There are frictional forces (even with a vacuum gap) reducing the propulsive force to

,  with friction coefficient  

Together, these correct the expression for the efficiency of

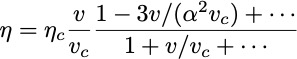
yellow ball For maximum power

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

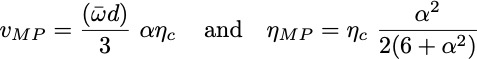
Fluctuations and linear Response

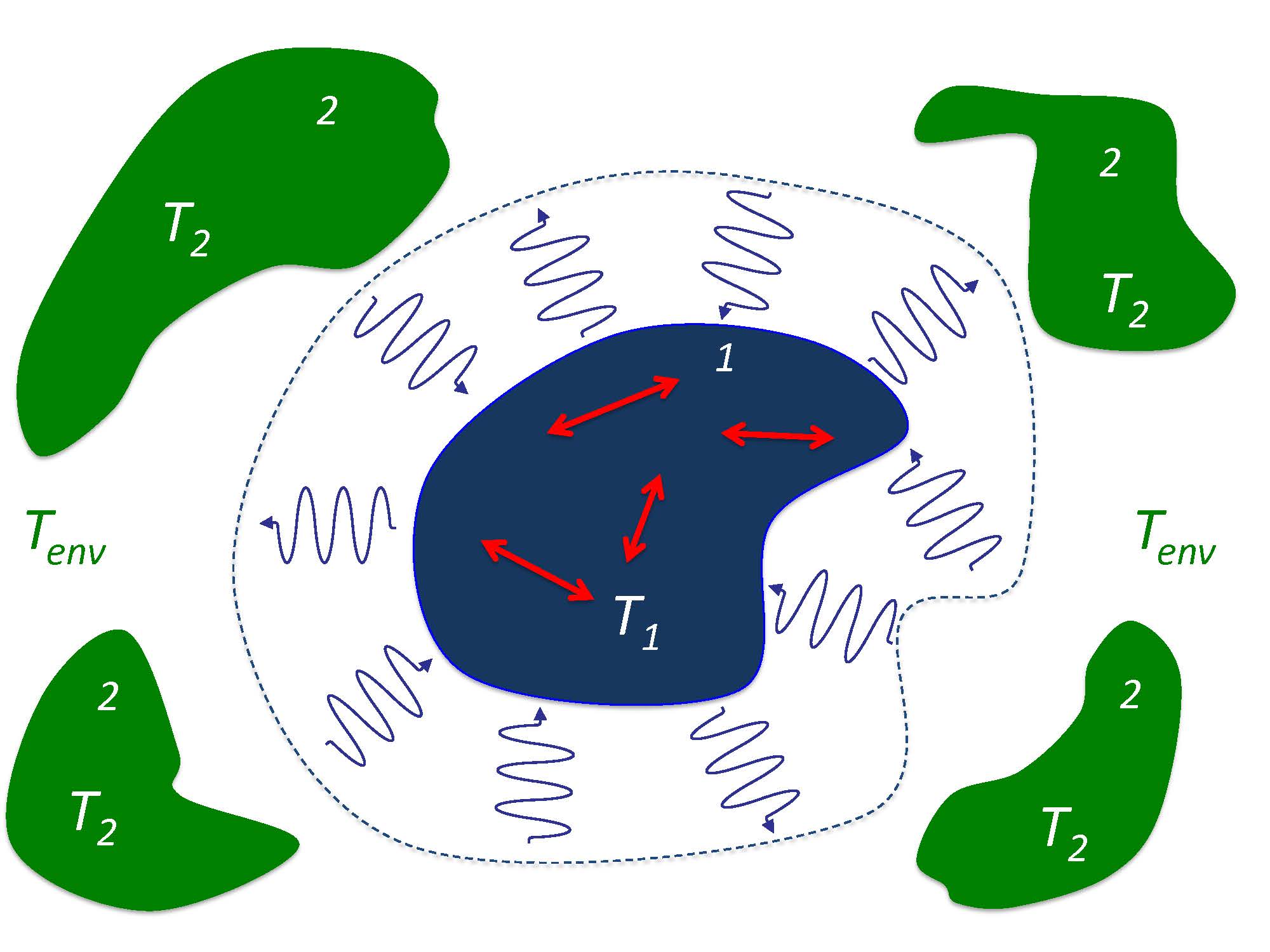
Rytov formalism allows computation of fluctuations in force and heat, both in and out of thermal equilibrium

          

Linear response (Onsager relations) connect equilibrium fluctuations to responses to small perturbations:

yellow ball Friction coefficient in vacuum at finite temperature

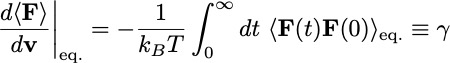
yellow ball Green Kubo relation (explicitly confirmed) provide coefficient of thermal conductivity

yellow ball  Onsager relation (relying of symmetry of mixed expectation values) give

 "Nonequilibrium Fluctuational QED: Heat Radiation, Heat Transfer and Force,"

V. Golyk, M. Krüger, and M. Kardar, Phys. Rev. B 88, 155117 (2013). (offline)