Growth/decay on a seascape
![]() Variations at each node are governed by time-scales from growth, migration, and fluctuation
Variations at each node are governed by time-scales from growth, migration, and fluctuation
_dt_-1.jpeg)
However, the variations of the mean population
are not directly sensitive to migration and stochasticity
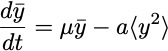
Assuming a separation of time scale in which evolution of
is slow enough for
to reach a quasi-state state, such that
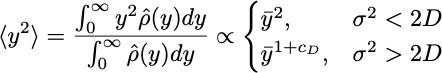
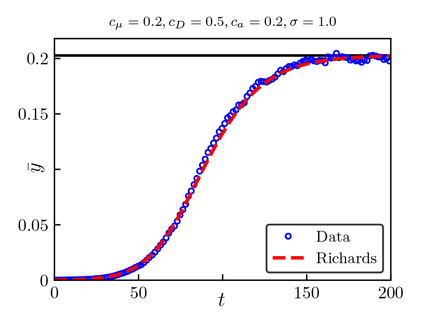
There is a mechanism to generate the empirical Richard's growth equation for sufficiently strong seascape stochasticity
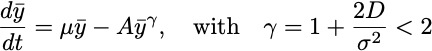
Note that the above conclusion holds if the node-level logistic growth equations are replaced with any analytic function of
![]() It is likely that some of these conclusions apply beyond the specific mean-field model, as:
It is likely that some of these conclusions apply beyond the specific mean-field model, as:
Fitness stochasticity (seascape) leads to very large local fluctuations,
Migration between sites somewhat smoothens the distribution, and
if the overall population changes slowly, can lead to broad (power-law) quasi-steady states of the form
![]()
Averaging any analytical local growth rule then leads to the Richard's equation for the variations of the mean population
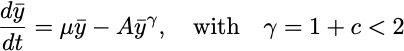
A potentially testable link between the local population distribution, and the global growth exponent.