![]() "A guide to first-passage processes," Sidney Redner, (CUP, NY, 1983)
"A guide to first-passage processes," Sidney Redner, (CUP, NY, 1983)
![]() "Kinetics of first-passage in a cone," E. Ben-Naim, P.L. Krapivsky, J. Phys. A 43, 495007 (2010)
"Kinetics of first-passage in a cone," E. Ben-Naim, P.L. Krapivsky, J. Phys. A 43, 495007 (2010)
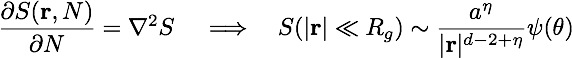
![]() The exponent η is the solution to the eigenvalue equation
The exponent η is the solution to the eigenvalue equation
Phantom polymer
with appropriate (scale invariant) boundary conditions on the bounding surfaces.
"A guide to first-passage processes," Sidney Redner, (CUP, NY, 1983)
"Kinetics of first-passage in a cone," E. Ben-Naim, P.L. Krapivsky, J. Phys. A 43, 495007 (2010)
The exponent η is the solution to the eigenvalue equation
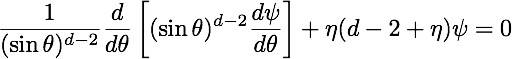
![]() Repulsive surfaces correspond to Dirichlet (absorbing) boundary condition ψ(θ)=0 . The corresponding values of η are:
Repulsive surfaces correspond to Dirichlet (absorbing) boundary condition ψ(θ)=0 . The corresponding values of η are:
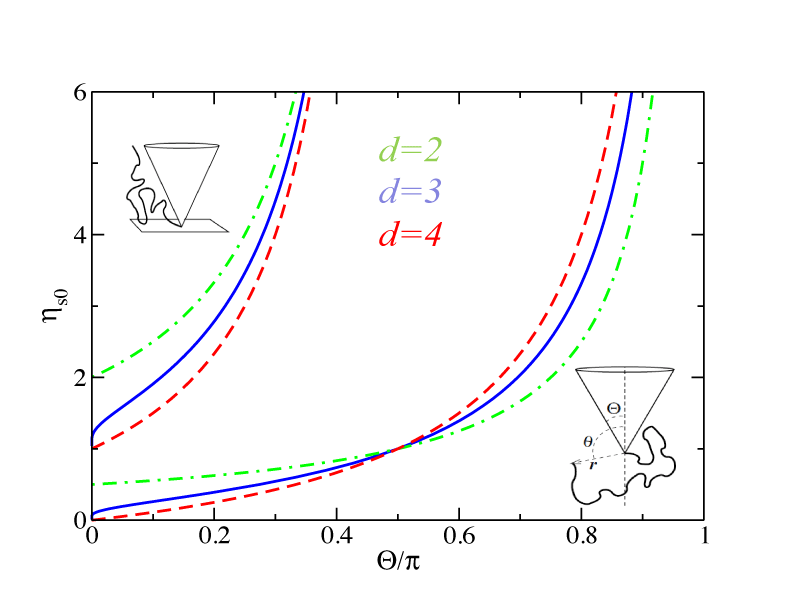
The resulting force amplitudes are:
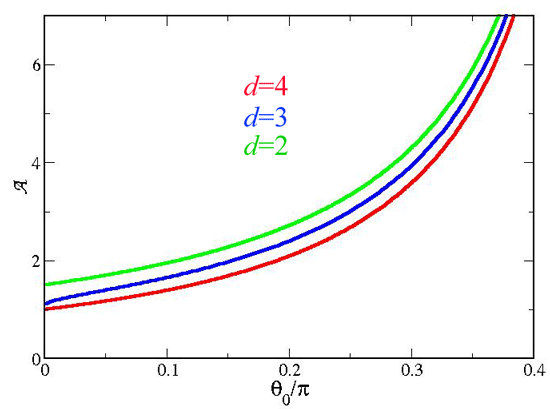
Note the singular behavior as the cone angle vanishes:
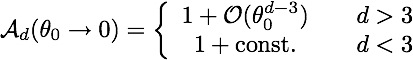
![]() Surfaces at depinning threshold correspond to Neumann (reflecting) boundary condition ψ'(θ)=0 .
Surfaces at depinning threshold correspond to Neumann (reflecting) boundary condition ψ'(θ)=0 .
The force constant A' depends on which surface is attractive/repulsive, e.g. D cone and N plate, or vice versa, as below for d=3;
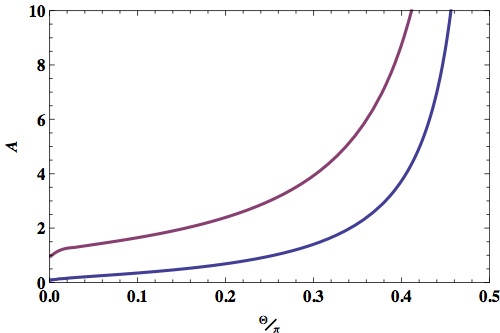
The interesting case of similar surface materials at the depinning transition is interesting, corresponding to A'=0 independent of shape!