![]() In Lifshitz (DLP) theory, unlike boundaries are obtained through an intervening medium with dielectric constant intermediate to the sides, as in the case of liquid helium climbing (wetting) a wall. (dielectric constants: solid > helium > air).
In Lifshitz (DLP) theory, unlike boundaries are obtained through an intervening medium with dielectric constant intermediate to the sides, as in the case of liquid helium climbing (wetting) a wall. (dielectric constants: solid > helium > air).
Repulsion/Levitation?
1. Boundary Conditions & Exotic materials
In Lifshitz (DLP) theory, unlike boundaries are obtained through an intervening medium with dielectric constant intermediate to the sides, as in the case of liquid helium climbing (wetting) a wall. (dielectric constants: solid > helium > air).

"Verification of Lifshitz theory of the van der Waals Potential using liquid-helium films,"
E.S. Sabisky and C.H. Anderson, Phys. Rev. A 7, 790 (1973)
"Measured long-range repulsive Casimir–Lifshitz forces,"
J. N. Munday, F. Capasso & V. A. Parsegian, Nature 457, 170 (2009) (gold, bromobenzene, silica)
Immersing MEMs in fluids is not practical. Is repulsion across vacuum possible?
"Van der Waals forces and zero-point energy for dielectric and permeable materials,"
T.H. Boyer, Phys. Rev. A 9, 2078 (1974) (large permittivity and large permeability repel)
A material with large permeability is required for repulsion, but in ordinary materials permeability is close to one.
Metamaterials, incorporating arrays of microengineered circuitry mimic, at certain frequencies, a strong magnetic response and have been proposed as candidates for Casimir repulsion across vacuum.
2. Repulsion via Geometry & Shape
![]() Abraham-Lorentz (+Casimir) model of electron: A spherical conducting shell of radius R ,
with charge e
Abraham-Lorentz (+Casimir) model of electron: A spherical conducting shell of radius R ,
with charge e
[ "Introductory remarks on quantum electrodynamics," H.B.G. Casimir, Physics 19, 846 (1956) ]
Balancing the repulsive Coulomb energy, with the (presumed attractive) Casimir energy:
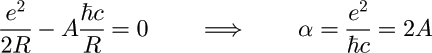
"Quantum Electromagnetic Zero-Point Energy of a Conducting Spherical Shell and the Casimir Model for a Charged Particle," T.H. Boyer, Phys. Rev. 174, 1764 (1968)
2A = - 0.09235 is negative! [also obtained by R. Balian and B. Duplantier (1977)]
Not only for spheres, but also rectangular boxes:
["Vacuum means of energy-momentum ...," S.G. Mamaev and N.N. Trunov, Sov. Phys. J. (USA) 22, 51 (1979)]
The "Casimir energy" of a parallelepiped changes sign with aspect ratio: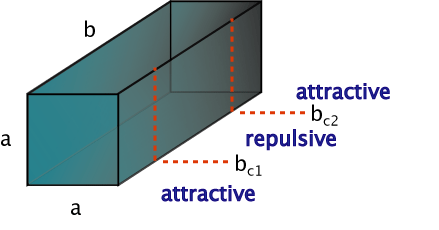
![]() This putative repulsive force has been proposed as yet another means of levitation:
This putative repulsive force has been proposed as yet another means of levitation:
"Attractive Casimir forces in a closed geometry,"
M. P. Hertzberg, R. L. Jaffe, M. Kardar, and A. Scardicchio, Phys. Rev. Lett. 95, 250402 (2005):
In the physically accessible geometry of a piston, the partition is always attracted to the closer side.
,
"Opposites Attract: A Theorem about the Casimir Force,"
O. Kenneth and I. Klich, Phys. Rev. Lett. 97, 160401 (2006) (two halfs of a cut sphere attract)
![]() Constrained repulsion?
Constrained repulsion?
"Casimir repulsion between metallic objects in vacuum,"
M. Levin, A.P. McCauley, A.W. Rodriguez, M.T.H. Reid, S.G. Johnson, Phys. Rev. Lett. 105, 090403 (2010)