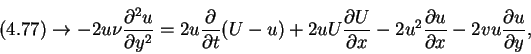Next: Approximate Method Based on
Up: Momentum and Energy Equations.
Previous: Momentum Integral
We multiply equation (4.77) and (4.78) respectively by 2u and
(U2-u2), so we have
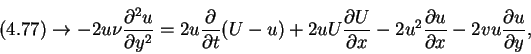 |
(94) |
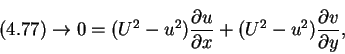 |
(95) |
and by adding them we obtain
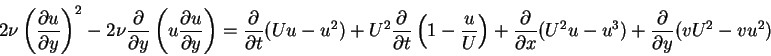 |
(96) |
If we integrate the equation above with respect to y from 0 to  ,
and if we take into account equations (4.79) to (4.83), we obtain
,
and if we take into account equations (4.79) to (4.83), we obtain
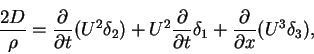 |
(97) |
since
v(U2-u2) and
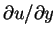 both tend to zero as y tends to infinite and the term
(vU2)y=0 is zero because it is assumed that there is no suction on the plate. The energy integral may also be regarded as an equation for the ``kinetic energy defect''
both tend to zero as y tends to infinite and the term
(vU2)y=0 is zero because it is assumed that there is no suction on the plate. The energy integral may also be regarded as an equation for the ``kinetic energy defect''
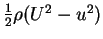 per unit volume, namely
per unit volume, namely
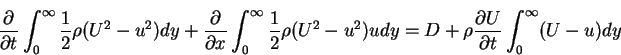 |
(98) |



Next: Approximate Method Based on
Up: Momentum and Energy Equations.
Previous: Momentum Integral
Karl P Burr
2003-03-12